“When a study’s result is statistically significant,” is a phrase you’ve likely heard someone use while discussing scientific research. But what exactly does that mean?
What calculation is behind statistical significance, and when is it helpful?
In this video, you will find answers to these questions, and more.
I will also explain how statistical significance can deceive us – if we forget what can not tell us.
This knowledge will empower you to critically review scientific studies and their results, allowing you to judge whether the arguments made are actually robust.
Statistical Significance
Firstly, let’s distinguish between ‘significance’ in everyday language and ‘statistical significance.’ We usually call something significant if it’s large or noteworthy.
However, ‘statistically significant’ doesn’t necessarily imply importance. Indeed, a statistically significant result can be quite minor and inconsequential in some cases.
Statistical significance becomes relevant when we use statistical methods to analyze quantitative datasets, especially to check if there’s a potential effect between two variables.
Imagine conducting an experiment where we manipulate one variable (like giving people a dietary supplement) and observe its effect on another (such as their training endurance).
If we find this effect to be statistically significant, it’s time to celebrate and head home, right? Well, it’s not that straightforward, but more on that later.
Statistical significance helps us determine the likelihood of a measurement result occurring by chance versus indicating a real effect.
If we deem a result statistically significant, it suggests that the result from the analysis of our sample might also apply to a wider population.

Statistical Significance and Sample Size
Typically, studies are not conducted with all individuals representing a specific group (i.e., the entire population) but with a sample from this population.
For example, if you conduct a survey, maybe 200 people participate. In an experiment, it might be 60. Or perhaps you’ve collected data from social media or businesses, involving 1000 or more subjects.
These samples always represent a population, such as all “citizens who are allowed to vote in the US” or all “higher education students” and so on. Researchers then aim to generalise the results of a survey or experiment with a small group from this population (i.e., the sample) to the whole population.
The size of these samples is crucial when interpreting significance tests.
The smaller the sample, the harder it is to detect a statistically significant relationship. This is because chance plays a greater role, and a very large effect must be present for chance to be statistically ruled out.
The larger the sample, the quicker statistically significant relationships can be measured. This is because larger samples more closely approximate the entire population, making a random result increasingly unlikely.
p-Value, Test Statistic, and Null Hypothesis
A central mathematical figure for testing statistical significance is the p-value. The p-value summarizes the results of a measurement and helps determine how likely it is that the result is due to chance or an actual effect. However, the magnitude of this effect cannot be determined from the p-value alone.
More specifically, the p-value is the probability that, assuming the null hypothesis is true, the test statistic will take the observed value or an even more extreme one.
Wait a moment – let’s slow down. Here we’ve introduced two new terms.
Test Statistic and Null Hypothesis
In a significance test, two hypotheses are crucial:
H0: There is no effect.
H1: There is an effect.
Through a significance test, the null hypothesis (H0) can be rejected.
For example, this might happen if the p-value is below 0.05. If so, there is reason to believe that an effect exists beyond mere chance.
The test statistic, a function of potential outcomes, defines a rejection region. If the result falls into this area, the null hypothesis is to be rejected.
The size of this region is determined by the significance level, usually set at 0.05, or 5%. This was once arbitrarily established by someone (named Ronald Fisher), but sometimes the significance level is set at 0.01, or 1%.
Whether a result is statistically significant largely depends on the significance level used. However, a p-value becomes increasingly impressive the smaller it is.
Determining Statistical Significance with the Student’s t-Test
A popular test for checking significance is the so-called Student’s t-Test. It’s not named so because it’s meant to drive students to despair.
Its inventor, William Sealy Gosset, initially published his ideas on this test under his alter ego “Student.”
The t-test is a hypothesis test and is often used with small samples. It aids in deciding whether to reject the null hypothesis. The null hypothesis is represented by the t-distribution, which offers an advantage over other functions like the normal distribution for small samples.
The t-test is applied to detect statistically significant differences between two variables. It can compare the mean of one variable with the mean of another. This is the most common application of the test.
Example:
We conduct an experiment with two groups of students. Both groups take the same English exam. However, one group studied using a flashcard app, while the other did not.
We might hypothesize that the group using the app achieved better results. In a t-test, we would compare the mean test scores of both groups.
It is also possible to compare the mean of a variable with a specific target or expected value.
The t-distribution also follows the shape of a bell curve.
For the t-test, a t-value is calculated using a specific formula. The formula for a t-test comparing a sample mean to a hypothetical mean (target value) is given by:
t = (x̄ – μ) / (s / √n)
- x̄ is the sample mean,
- μ is the hypothetical mean (target value),
- s is the sample standard deviation, and
- n is the sample size.
The t-value
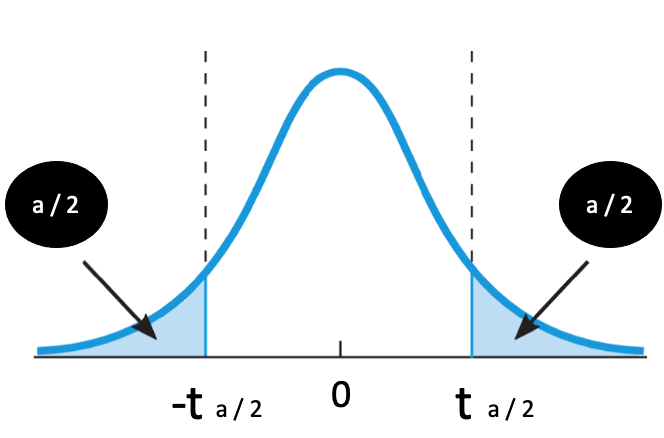
The calculated t-value is then compared to the critical values from the t-distribution, based on the degrees of freedom (which, in this context, is typically n – 1) and the desired level of significance. If the t-value is close to zero, it indicates no significant difference between the sample mean and the hypothetical mean (target value). If the t-value falls in the critical region at the tails of the distribution, the difference is significant enough that the null hypothesis (no difference) should be rejected, suggesting an effect.
The critical regions (α/2) are determined by the significance level. For a two-tailed test, with a significance level of 5%, you would have 2.5% in the left tail and 2.5% in the right tail of the distribution. A two-tailed test is used when the hypothesis is non-directional (“There is some effect”). The test is one-sided when the hypothesis is directional (“There is a positive/negative effect”). In that case, the entire α (e.g., 5%) is allocated to one side of the distribution, depending on the direction of the hypothesis.
Summary
Statistical Significance is an important tool to assess the results of quantitative studies that aim to measure an effect between two variables. It tells us how probable it is that our result is based on an actual effect, or that the result was based on mere chance.
However, statistical significance does not tell us how big an effect is. This means that even though an effect is statistically significant, the effect might be very minimal. We can also never say with absolute certainty that the result was not created by chance – even with a statistically significant result, there is still a small probability left that there is no effect.
